This is part one of a two-part series on risk frameworks.
I’m going to present a couple of simple frameworks that I use to think about risk. In both cases, the concepts are very straightforward, but the terminology is my own.
The first framework is a practical way to implement mean-variance optimization (it’s a heuristic to help you avoid making the worst mistakes). The second framework is a practical way to implement the Kelly Criterion (that’s tomorrow’s post).
Harry Markowitz won the Nobel Prize in 1990 for his work on mean-variance optimization theory (“Portfolio Choice”, Journal of Finance, 1952). William Sharpe and Merton Miller extended Markowitz’s work in the 1960s to create the Capital Asset Pricing Model. They shared the Nobel with Markowitz in 1990.
Applying mean-variance optimization, however, is no easy task. I present here a simple variant of mean-variance optimization theory that ensures, at a minimum, that you don’t make egregious mistakes.
To make a poker analogy, there is a perfect way to play (game theoretic optimality), but almost every player’s game suffers from serious errors of logic and they would be better off eliminating all of these errors before proceeding to a study of optimal play.
I think about mean and variance in the following way:
If given a choice among two investments with equal variance and I choose the investment with the lower return, I have committed an ERROR IN EXPECTATION.
If given a choice among two investments that have the same expected return, and I choose the one with higher variance, I have committed an ERROR IN VARIANCE.
Since both of these mistakes are straightforward errors in logic, you would think they’d be easy to avoid. They aren’t necessarily.
I commit errors of both types, but having the framework allows me to be concrete about the mistakes I’m making. For example, you might make a mistake to help a friend, or for entertainment, or for stress minimization, but you should be able to formalize the cost of the mistake.
Compound interest, which Albert Einstein termed “the strongest force in the universe,” is well understood by everyone who considers themselves financial literate. A well-invested dollar expands its tentacles over time, as not just the initial dollar, but also the returns that the dollar yields, are the progenitor of yet more dollars, ad infinitum. If one is able to successfully invest one’s dollars at a modest positive returns, and one is able to successfully navigate the penalties of variance, the result is a beautiful exponential curve.
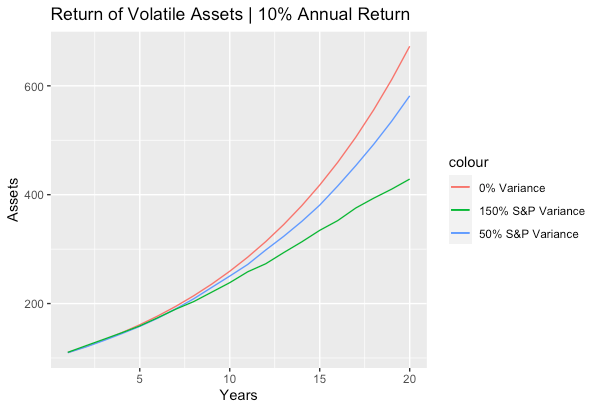
Below is a graph of 10% returns compounded with no variance (a savings account with 10% interest), with 13% standard deviation (equivalent to roughly 50% of S+P variance), and with 23% standard deviation (equivalent to 150% of S+P variance).
The above graph shows the beautiful power of exponential growth. Incidentally, it also shows the annoyance of variance drag, the phenomena whereby a pure exponential growth (the first curve) is diluted by variance. The geometric mean return – what one truly cares about – is approximately equal to the arithmetic mean (10%) minus ½ of the variance from the arithmetic mean.
Variance drag is the reason you should spend a lot of time thinking about ERRORS IN VARIANCE.
Revisiting the concept, we can expand it to think in terms of near neighbors or combinations of similar assets. In general, if you are wedded to one particular investment idea, it’s a good idea to ask yourself: “Is there another investment or trade that is very similar to this investment or trade, such that I’m almost indifferent between the two?” If there is, you’re probably better off splitting your investment between the two.
There are applications of ERRORS IN EXPECTATION and ERRORS IN VARIANCE that relate to market microstructure and practical trading. For example, suppose you decide that you want to go long DKNG stock. It’s trading at $42. You could just go long the stock, but there are other options. For example, it’s theoretically possible to have a program that ensures that, if you want to get into the stock and there’s a way that MUST BE BETTER than getting in an $42, you do that instead. For example, if I could buy a call option at a strike of $20 for Jan 2025 expiration for $22, that must be better (because I save money in all the states of the world where DKNG is below $20 by Jan 25). That’s a simple example (Citadel is there before you, in that case), but thinking in these terms can often save you money in trade implementation.